背包问题

先从栗子出发，你是一个有理想的吃货，你的肚子只能容纳 500g 的食物，为了保证你得到的价值（营养）最大化，有以下几份食物可以选择

食物 质量/weight （100g） 价值/value（10g）
米饭 2 4
黄瓜 1 5
西红柿 1 8
牛肉 3 10

动动吃货的小脑筋，就知道，营养价值最大化的选择是
牛肉+黄瓜+西红柿 共 23（10g）营养！
可是该怎么使用程序计算出答案呢？

思路

肚子的资源有限，对每一种食物有两种选择：吃或者不吃。
判断的依据有两点：

（1）肚子能否装得下食物？

（2）吃他的价值，是否比不吃他的价值大？大则吃下，不大则不吃。

假设 d（i，w）表示肚子剩 w（g）时，有 i 样食物可供选择，我们能得到的最大价值。i 表示第 i 样食物。我们需要求的是 d（4，5）

根据上面的逻辑（1）

  • 如果肚子装不下，因为食物 i 没装进去，那么 d(i,w) = d(i-1,w)

  • 肚子装得下，那我需要判断 [不放] d(i-1,w) 和 [放] d(i-1,w-w[i])+v[i] 谁大。

结合上面两条规律，我们得到:

状态转移方程式

d(i, w)=max{ d(i-1, w), d(i-1,w-w[i]) + v[i] }

我们给每样食物加上序号

序号 食物 质量/weight （100g） 价值/value（10g）
1 米饭 2 4
2 黄瓜 1 5
3 西红柿 1 8
4 牛肉 3 10

假如我们考虑吃或不吃从下向上按照序号顺序 4，3，2，1

d（4，5）表示只有牛肉、西红柿、黄瓜、米饭可以选择时，能得到的最大价值。考虑是否放牛肉（3 kg），所以如果我知道 d（3，5）和 d（3，2），我就能得到 d（4，5）

d(4 , 5)=max{ d(3,5) , d(3,5-3) }=max{ d(3,5) , d(3,2) + 10}

d（3，5）表示只有西红柿、黄瓜、米饭可以选择时，能得到的最大价值。考虑是否放西红柿（1 kg），如果我知道 d（2，5）和 d（2，4），我就能得到 d（3，5）

d(3 , 5)=max{d(2,5) , d(2,4)}

按照上面的往下分解,最终都会指向 d(0,w)～逻辑如下图：

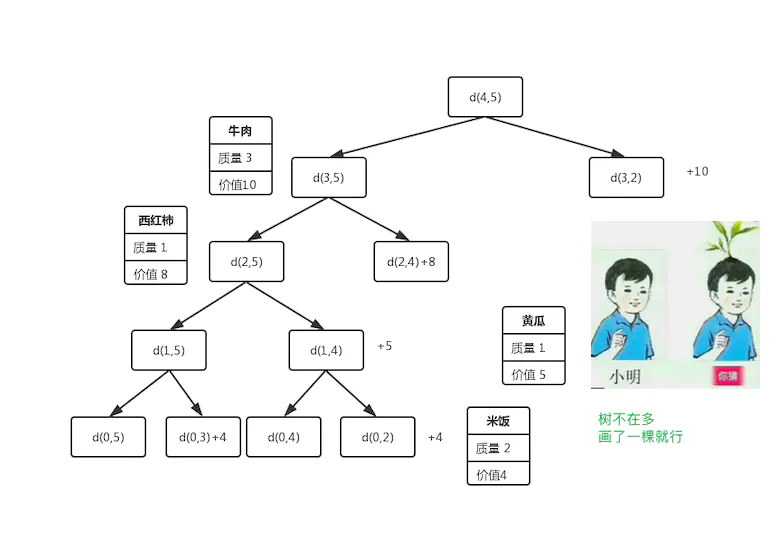
d(0,w)代表选 0 件物品的放入背包容量为 w 的背包的最大价值，所以为 0。d(i,0)代表选 i 件物品放入背包容量为 0 的背包的最大价值，也为 0。

将树图的 d 值继续整理得到最优价值表

质量/weight（100g） 价值/value（10g） i\w 0 1 2 3 4 5
1 8 3 0 8 13 13 17 17
1 5 2 0 5 5 9 9 9
2 4 1 0 0 4 4 4 4
3 10 4 0 8 13 13 18 23
0 0 0 0 0 0 0 0 0 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
var value = [5, 8, 4, 10],
    size = [1, 1, 2, 3],
    d = [],
    n = 4,
    C = 5;
//初始化数组
for (var k = 0; k <= n; ++k) {
    d[k] = [];
}
for (var i = 0; i <= n; ++i) {
    for (var w = 0; w <= C; ++w) {
        d[i][w] = (i == 0) ? 0 : d[i - 1][w];
        if (i > 0 && w >= size[i - 1])
            d[i][w] = Math.max(d[i - 1][w], d[i - 1][w - size[i - 1]] + value[i - 1]);
    }
}

 console.log(d[4][5])//23

总结

01 背包问题的这种解法让我感受到了递归的强大，将大问题转换成小问题，然后得到小问题的答案向上求解！

2. 例题

链接：https://www.nowcoder.com/questionTerminal/9ba85699e2824bc29166c92561da77fa
来源：牛客网
一种双核 CPU 的两个核能够同时的处理任务，现在有 n 个已知数据量的任务需要交给 CPU 处理，假设已知 CPU 的每个核 1 秒可以处理 1kb，每个核同时只能处理一项任务。n 个任务可以按照任意顺序放入 CPU 进行处理，现在需要设计一个方案让 CPU 处理完这批任务所需的时间最少，求这个最小的时间。

3. 资料

动态规划之背包问题（一）

动态规划之 01 背包问题–表格思路来源

通过金矿模型介绍动态规划